Le Radici Quadrate
In matematica, la radice quadrata di un numero  è un
numero
è un
numero  tale che il
suo quadrato sia
tale che il
suo quadrato sia  , ovvero tale
che
, ovvero tale
che  . Ogni
numero reale non negativo ha un'unica radice quadrata non negativa, chiamata radice quadrata principale, che viene rappresentata simbolicamente come
. Ogni
numero reale non negativo ha un'unica radice quadrata non negativa, chiamata radice quadrata principale, che viene rappresentata simbolicamente come  o, nella notazione
esponenziale, come
o, nella notazione
esponenziale, come 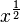 . Ogni numero reale
maggiore di zero ha due radici quadrate distinte, quella principale e il suo opposto, ovvero
. Ogni numero reale
maggiore di zero ha due radici quadrate distinte, quella principale e il suo opposto, ovvero  e
e  .
.
Il concetto di radice quadrata può essere esteso ai numeri negativi nell'ambito dei numeri complessi. Più generalmente, il concetto di radice quadrata può essere esteso in qualunque contesto in cui sia ben definita la nozione di quadrato di un elemento.
Le Proprietà
La funzione radice quadrata principale ha una grande utilità, perché pone in
corrispondenza l'insieme dei numeri reali non negativi 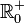 con se stesso; si individua scrivendo
con se stesso; si individua scrivendo  o anche
o anche  . Più precisamente questa endofunzione entro
. Più precisamente questa endofunzione entro 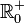 è una biiezione crescente e continua.
è una biiezione crescente e continua.
L'equazione  ha solo due soluzioni,
ha solo due soluzioni,  e
e  . In altre parole la funzione radice quadrata principale è una permutazione (cioè una endofunzione
biiettiva) di
. In altre parole la funzione radice quadrata principale è una permutazione (cioè una endofunzione
biiettiva) di 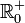 avente
avente 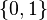 come insieme dei punti fissi.
come insieme dei punti fissi.
Per ogni due numeri reali positivi  e
e  si trovano subito le identità
si trovano subito le identità
Queste uguaglianze sono in sintonia con il fatto che la funzione radice quadrata fa corrispondere all'area di
un quadrato la lunghezza del suo lato. Esse inoltre per 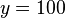 diventano
diventano
-
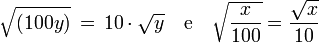 .
.
Queste uguaglianze implicano che per tabulare nella notazione decimale i valori assunti dalla funzione radice quadrata
principale è sufficiente conoscere i suoi valori nell'intervallo  .
.
Per ogni numero reale  si trova che
si trova che
Si supponga che  e
e  siano reali e che
siano reali e che  , e che si voglia ottenere la
, e che si voglia ottenere la  . Un errore comune consiste nell'estrarre la radice quadrata e dedurre che
. Un errore comune consiste nell'estrarre la radice quadrata e dedurre che  . Questo non è lecito, in
quanto la radice quadrata principale di
. Questo non è lecito, in
quanto la radice quadrata principale di  non
è
non
è  , ma il valore
assoluto
, ma il valore
assoluto  , come dice l'uguaglianza
precedente. Non commettendo questo errore si potrebbe concludere che
, come dice l'uguaglianza
precedente. Non commettendo questo errore si potrebbe concludere che  , o equivalentemente
, o equivalentemente  .
.
L'uguaglianza che segue è utile in molti passi del calcolo infinitesimale, ad esempio per dimostrare che la funzione radice quadrata è continua e differenziabile, o per calcolare certilimiti:
valida per tutte le coppie di interi non negativi  e
e  che non sono entrambi zero.
che non sono entrambi zero.
La funzione  ha il seguente grafico, ottenibile da una metà di parabola avente come asse l'asse
delle
ha il seguente grafico, ottenibile da una metà di parabola avente come asse l'asse
delle  .
.

Questa funzione, continua per tutti gli  non negativi, è differenziabile per tutti gli
non negativi, è differenziabile per tutti gli  positivi, ma non è differenziabile per
positivi, ma non è differenziabile per  , poiché la pendenza della tangente nel corrispondente punto tende a
, poiché la pendenza della tangente nel corrispondente punto tende a  ).
).
La derivata della funzione è data da
La serie di Taylor di  in un intorno di
in un intorno di  si può ottenere servendosi del teorema binomiale:
si può ottenere servendosi del teorema binomiale:
per 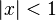 .
.
 Ricerche
Ricerche




