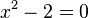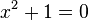Equazioni

Un'equazione (dal latino aequo, rendere uguale), in matematica, è una uguaglianza tra due espressioni contenenti una o piùvariabili, dette incognite.

Se un'equazione ha n incognite, allora n elementi ordinati che, se sostituiti alle corrispondenti incognite, rendono vera l'uguaglianza ottenuta dall'equazione sono detti una soluzione dell'equazione. Risolvere un'equazione significa individuare l'insieme di tutte le soluzioni dell'equazione.

Il dominio (o insieme di definizione) delle variabili incognite è l'insieme degli elementi per cui le espressioni ad ambo i membri dell'equazione sono definite. L'insieme delle soluzioni è condizionato dal dominio: per esempio l'equazione

$x^2 - 2 = 0$

non ammette soluzioni se il dominio è l'insieme dei numeri razionali, mentre ammette due soluzioni nei numeri reali, che possono essere scritte come $\pm \sqrt{2}$ . Analogamente, l'equazione

$x^2 + 1 = 0$

non possiede soluzioni reali ma è risolvibile se il dominio è il campo dei numeri complessi.

Tipicamente in un'equazione compaiono, oltre alle incognite, dei coefficienti noti, che, se non sono esplicitati nel loro valore numerico, sono indicati in genere con le lettere $a$ , $b$ , $c$ ... mentre alle variabili incognite sono convenzionalmente attribuite le ultime lettere dell'alfabeto ( $x$ , $y$ , $z$ ...).

Le soluzioni di un'equazione vengono generalmente indicate esplicitando le incognite delle espressioni che contengano le costanti ed eventuali parametri arbitrari. Ad esempio, la soluzione dell'equazione

$ax + 2 = b$

dove a è un parametro non nullo, e il dominio è l'insieme dei numeri reali, si scrive come

$x = \frac{b-2}{a}$

Un'equazione si dice:

determinata se ammette un numero finito di soluzioni, in tal caso l'insieme soluzione sarà discreto, formato da un numero finito di elementi.
impossibile se non ammette soluzioni, in tal caso l'insieme soluzione sarà l'insieme vuoto.
identità se ha come soluzioni tutto il dominio, in tal caso l'insieme soluzione sarà uguale all'insieme dominio.
indeterminata se il numero delle soluzioni è infinito ma non coincide con tutto il dominio, in tal caso l'insieme soluzione sarà infinito e diverso dall'insieme dominio.

Dal Teorema fondamentale dell'algebra, segue immediatamente che un'equazione polinomiale (ovvero formata da un polinomio eguagliato a zero, in una variabile) di grado n ammette sempre n soluzioni in campo complesso, di cui alcune possono essere multiple. In altre parole, un'equazione di grado $n$ ammette almeno 1 soluzione e al massimo $n$ soluzioni complesse differenti.

Per il Teorema di Abel-Ruffini, non esiste una formula generale per esprimere le radici delle equazioni polinomiali di grado 5 o superiore tramite una formula per radicali. Viceversa le equazioni di primo grado, secondo grado, terzo grado e quarto grado ammettono una formula risolutiva. Casi particolari di equazioni di grado superiore al quarto possono comunque ammettere una formula risolutiva.

Il Metodo delle tangenti di Newton, sotto determinate ipotesi, fornisce un algoritmo per la risoluzione numerica delle equazioni. Un altro algoritmo con ipotesi più generali è il metodo di bisezione. Le soluzioni trovate mediante metodi numerici vengono chiamate approssimate in contrapposizione alle soluzioni date da formule chiuse che vengono chiamate esatte. La nomenclatura è in parte fuorviante perché i metodi approssimati possono, in alcuni casi, determinare in maniera più precisa e più veloce le soluzioni numeriche di una equazione rispetto alle formule chiuse.

Una prima classificazione delle equazioni può avvenire in questo modo:

equazioni algebriche, riconducibili a polinomi;
equazioni trascendenti, non riconducibili a polinomi;
equazioni funzionali, in cui le incognite sono funzioni.

Le equazioni algebriche possono essere divise in vari gruppi in base alle loro caratteristiche; è necessario ricordare che un'equazione deve appartenere ad almeno e solo una delle categorie per ogni gruppo.

In base al grado del polinomio:

equazioni di 1º grado o equazioni lineari;
equazioni di 2º grado o equazioni quadratiche;
equazioni di 3º grado o equazioni cubiche;
equazioni di 4º grado o equazioni quartiche;
equazioni di 5º grado o equazioni quintiche;
e così via.

Possono inoltre essere divise in base alla presenza di incognite al radicando di radici:

equazioni non irrazionali;
equazioni irrazionali, contenenti radici con incognite al radicando, si classificano in base all'indice della radice:
- indice pari;
- indice dispari.

Le equazioni trascendenti coinvolgono almeno un'incognita come argomento di una funzione non polinomiale. Le più comuni categorie di equazioni trascendenti sono:

equazioni trigonometriche, in cui almeno un'incognita è presente come argomento di funzioni trigonometriche;
equazioni esponenziali, in cui almeno un'incognita è presente come argomento di funzioni esponenziali;
equazioni logaritmiche, in cui almeno un'incognita è presente come argomento di logaritmi.

Le equazioni funzionali hanno almeno un'incognita che è una funzione. Le più comuni categorie di equazioni funzionali sono:

equazioni differenziali, se contengono derivate della funzione incognita;
equazioni integrali, se contengono integrali della funzione incognita.

In base alla presenza di altre espressioni letterali tutte le equazioni possono essere divise in:

equazioni numeriche, contengono solo espressioni numeriche e l'incognita;
equazioni parametriche, in cui le incognite sono funzioni espresse in funzione di uno o più parametri